- Published on
- views・
Paper 3 - Implementing Procedural Dungeon Generation In Top-Down Games Using Wave Function Collapse (WFC) & Binary Space Partitioning (BSP)
- Authors
- Name
- shaancoding
- @ShaanCoding
Abstract
In this paper, we will introduce & explore a solution to creating humanized realistic dungeons or maps in the 2D top-down rogue-like genre. This paper will explore a proposed solution, combining both the strengths of Binary Space Partitioning and Wave Function Collapse to create a highly flexible yet robust algorithm capable of autonomous procedural world generation with minimal errors.
Introduction
Procedural map generation in rogue-like games has been a staple since the conception of the genre in the 1980s. While rogue-likes can take a range of different forms, aesthetics & game-play mechanics, they all share the common goal of trying to transverse a dungeon to the next level. Early on in the genre's conception, game-play designers paid close attention to the hardware limitations consumer PCs contained as every byte counted, with hardware space being limited. Game designers, as a result, opted to use & discovered the world of procedural content generation to increase both replayability and customizability.
While in the genre's early conception, procedural content generation (PCG) was necessary due to hardware constraints. The link between procedural world generation (PWG) and rogue-likes has been closely linked ever since and has become an iconic key aspect of the genre's allure. Through constant iterations and innovation in procedural content generation methods, this field has slowly but steadily improved on the pitfalls these early algorithms contained, increasing both overall accuracy & performance. However, these modern algorithms are still incredibly performance heavy and require significant processing power to generate and evaluate playable maps unsupervised in real-time.
In this paper, we intend to implement & evaluate our own programmatic procedural world generation function capable of both variation, customization, and aesthetics based on Wave Function Collapse (WFC) Functions & Binary Space Partitioning (BSP).
Identifying The Problem
Multiple procedural world-generation techniques have been used over the decades, such as Markov chains, cellular automata, BSP trees, texture synthesis, machine learning & many many more. These, in one way or another, have been lacking in either customizability, accuracy, or speed. While each of these proposed listed models has its associated benefits and weaknesses, a well-rounded algorithm addressing all three factors has not been achieved. Whilst some have strived for great performance many of them as a result have sacrificed uniqueness and/or playability and vice-versa. Listed in the table below is a detailed breakdown of such historic algorithms with their associated strengths, weaknesses & features.
| Technique | Pros | Cons |
|---|---|---|
| Markov Chains | Fast, aesthetically pleasing & varied, output statistically resembles similar things to its given components, reliant on clearly defined statistical properties (not a black box) | Reliant on statistical properties on a small scale, this fails to see long term dependency of the entire map and occasionally causes unsolvable maps, needs active repair function (such as backtracking) to fix unsolvable sections |
| Cellular Automata | Fast, simple, low cost, creates 'natural' looking cave environments | Unstructured, chaotic, lacks overarching control or long term understanding, cannot create dungeons, can create unsolvable levels & requires an active repair function |
| Machine Learning | High variety, capable of capturing statistical patterns of real levels, can recognize overarching level design patterns, requires minimal coding, can be reused for many applications with minimal editing | Requires an active repair function, is highly performance intensive in both CPU, Memory & RAM, often fails to capture underlying rules of a level, is a "black box" where the predicted output has no way of debugging or future understanding - i.e., an input comes in and an input goes out, requires huge data sets & clean training data to set up |
| BSP Trees | Good, highly effective, creates iconic cube dungeons, very easy to program, space aware, requires minimal fixing (back-tracking to add to pathways), is simplistic in concepts & very easy to debug & modify | Variation is limited, cannot create 'real' procedural maps (it is still pre-defined), levels are typically required to be rectangular / non-continuous |
This research paper aims to explore & attempt to solve the issue of creating aesthetically pleasing yet optimized dungeon maps through autonomous means using Procedural World Generation (PWG) methods.
Settings For Experiment
Setup & Tools
The tools required for this experiment are minimal. For this application to run we require:
- Minecraft (Version 1.6.4) Installed
- .NET Framework
- Visual Studio 2019 Community / Enterprise Edition
- Benchmarking Software (E.g. A Timer & Visual Studio)
Proposed Solution
The algorithm proposed to create unique aesthetically pleasing maps and have a substantial degree of conformity, adhering to high-level map design rules, and consistency and division between levels consists of two algorithms—the Wave Function Collapse (WFC) Function as well as Binary Space Partitioning (BSP).
Through WFC and BSP, we can, as a result, leverage the benefits of both algorithms while also increasing performance.Through the recursive nature of Wave Function collapse, parallelization or optimization of the algorithm alone is not feasible. It uses an exorbitant amount of memory and processing power to compute exponentially increasing as the size of the grid increases.
However, we can divide the map into several blocks or dungeon sets through binary space partitioning, which all contain unique instances of Wave Function collapse. Through this, we can contain the rigid structure of binary space partitioning, having its iconic rectangular dungeon designs in addition to having its easy back-tracking algorithm to combine levels and with the strengths of Wave Function collapse, making each dungeon room unique and distinct from the rest, while still being playable.
Through the separation of the map into several Wave Function collapse chunks instead of one large field, we also allow the possibility of parallelization where we can run multiple instances of Wave Function collapse concurrently, increasing overall performance as well as reducing the overall time & space complexity required to run this algorithm.
Through this proposed solution, we also eliminate the downfalls of binary space partitioning, where variation is typically limited and allows continuous / non-rectangular maps to be implemented if desired. Wave Function collapse, in addition, allows us to create unique, distinctive maps with a pseudo-human aesthetic, being aesthetically familiar to hand-designed levels.
This, paired with the customizability, with outputs being dependent on the conditional restrictions placed on neighboring nodes as well as the associated weights allows our algorithm to be significantly more flexible than other conventional map generation methods, such as machine learning, while also containing significantly better performance & playability metrics compared to other methods, such as; Machine learning, cellular automata, Markov chains & texture synthesis when used on their own.
Implementation
The proposed implementation of the algorithm is a hybrid design, implementing both Wave Function Collapse (WFC) and Binary Search Trees (BSP). The map is uniquely sectioned into several areas or rooms through a quick run of the BSP algorithm on map initialization. These rooms are then traversed through and generated through Wave Function Collapse. The flowchart for the proposed algorithm is given below.
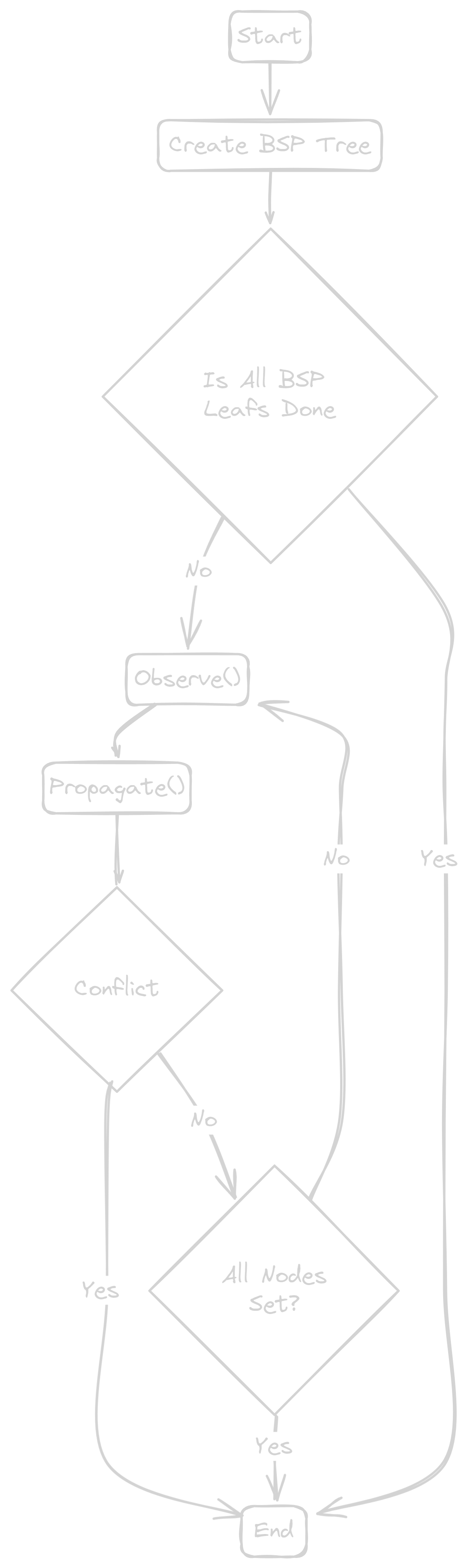
Figure 2: Proposed Diagram Flowchart
Alternatively, the pseudocode implementation of the algorithm is also provided, available below:
1Figure 3: Proposed Diagram Pseudocode
After this pseudocode was designed, the code was then implemented in Minecraft using C#. This platform was chosen as it is straightforward to use, debug & quickly prototype and edit input values for the WFC algorithm with minimal effort. It, in addition, is also a platform the scientists in this paper are deeply familiar with.
Results
The figure below shows the input given to the Wave Function Collapse section of the algorithm. The white represents walls, chests represent treasures, TNT represents hazards & water represents water. The algorithm takes this 25 x 25 grid and divides them into 5x5 kernels or sections, which then can be rotated, transposed, and combined with other kernels within each given binary space partition block or 'room.' The selected kernel is chosen based on quasi-randomness emulating entropy with each block recursively comparing itself to its neighbors until the kernels state converges.

Figure 4: Wave Function Collapse + BSP Input
The algorithm then takes the given Wave Function Collapse input and the given output size, in this case, 50x50, and firstly partitions the map into several binary space partitions, signified in green, in figure 4. Once these binary space partitions are initialized, each one is then propagated and initialized through the input given by the wave function collapse algorithm in the figure shown above, figure 3.
In the figure shown below, figure 4, we can see the output of the resultant algorithm 50% completed. This shows both the raw binary space partitioning as well as the detailed & converged wave function collapse rooms respectively.
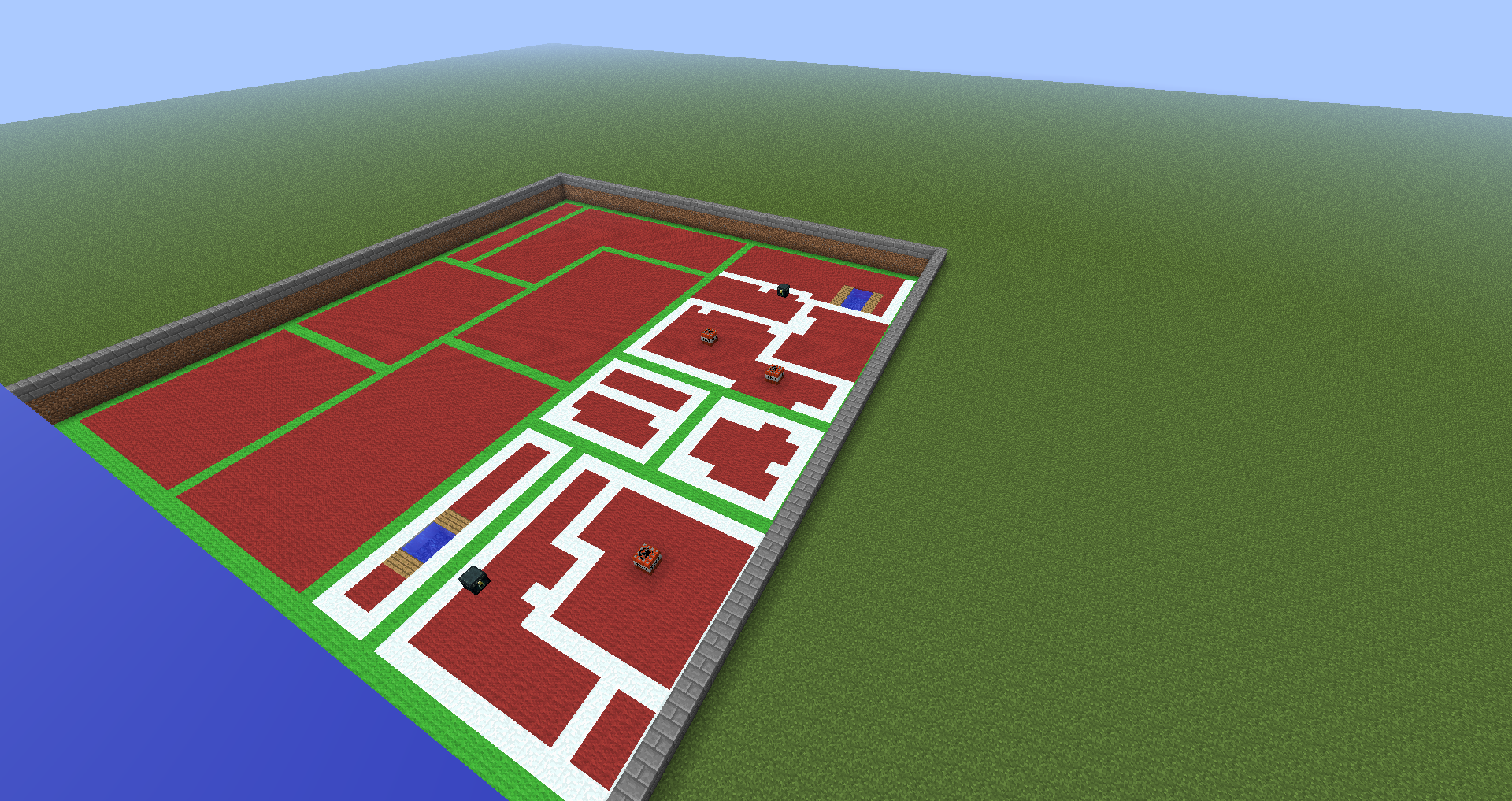
Figure 5: Wave Function Collapse + BSP Output
Discussion
The resultant of the proposed combined algorithm utilizing both Wave Function Collapse and Binary Space Partitioning is shown below. The implementation of This algorithm due to time constraints and the game engine used resulted in the very slow implementation of the proposed algorithm, not containing parallelization to run more efficiently. This, however, benchmarked compared to non-binary space partitioned algorithms led to exciting results. While WFC on its own led to impressive results, creating humanistic & aesthetically pleasing levels. The time taken for the algorithm to determine the value of each node or 'block' increased exponentially as the size of the input and output increased. This is most likely due to the recursive nature of Wave Function Collapse, and by reducing the size of n, the algorithm significantly increases in speed.
This implemented algorithm also had issues with it being buggy & inconsistent for increasing complex designs with its back-tracking algorithm spiraling into infinite loops occasionally exiting due to luck from the pseudo-entropy randomness given. This is most likely a result of the short time frame given for the implementation of the wave function collapse algorithm and is not likely caused due to the simultaneous use of binary space partitioning & wave function collapse.
The use of binary space partitioning also allowed these rooms to continue to keep the traditional rectangular dungeon room design standard from BSP while also allowing these rooms to remain unique and not be provided by a list of pre-assembled rooms, increasing variation while also maintaining playability.
An additional implementation/modification of the back-tracking algorithm for adding corridors may be needed, whereas it also adds or seals dungeon rooms in case of WFC failure. This issue can be highlighted in the figure given below circled in yellow, where the WFC algorithm fails to properly seal the room.
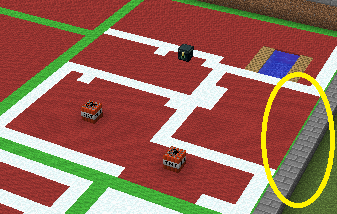
Figure 6: Wave Function Collapse + BSP Error
The Future
Whilst this solution did have it's pitfalls, specifically with speed, due to the lack of optimization. This solution is definitely sound and has the opportunity to scale into a highly successful and robust algorithm in the future. Further proposed work in this algorithm in the future include:
- Parallelization, allows the algorithm to perform significantly faster and asynchronously from each other, allowing each binary space partition to wave function collapse simultaneously instead of contiguously
- Further data structure & time-complexity optimization, utilizing divide & conquer algorithms and optimizing the overall time complexity
- Hardware multi-threading utilizing CUDA Cores or FPGAs as dedicated hardware
- The addition of a convolutional neural network model to evaluate the size & difficulty of maps for the unsupervised creation of maps with consistent playability for users
Conclusion
To conclude, this experiment was an overall success; the combination of Wave Function Collapse & Binary State Partitioning resulted in a highly flexible & robust algorithm capable of significant parallelization, accuracy, aesthetics, uniformity & uniqueness while maintaining both high levels map design rules as well as containing intricate details. The algorithm, however, had shortfalls, specifically with speed & its recursive back-tracking algorithm where it occasionally fails and spirals into an infinite loop; however, with adjustments & better data structure optimization, and further implementation of advanced algorithmic designs such as divide & conquer techniques, this algorithm can significantly improve.
