- Published on
- views・
Paper 2 - Programmatic Procedural Map Generation Using Wave Collapse Functions (WFC) For Game Development In Top-Down
- Authors
- Name
- shaancoding
- @ShaanCoding
Abstract
In this paper, we will explore the issue of programmatic procedural map generation for video games in the 2D top-down rogue-like genre. Through this paper, we will cover multiple forms of procedural content generation (PCG) in the indie & professional game development community as well as propose & lay out our plans for such a system using the Wave Form Collapse (WFC) function.
Introduction
Procedural map generation has been a staple for rouge-like games since the early conceptions of the video game genre in the 1980s. Rouge-likes can take take variety of different forms, aesthetics and game-play mechanics, however, they all share the goal of trying to transverse a dungeon or an arena to the next level. Early on in the genre’s conception, game-play designers played close attention to the hardware limitations consumers pcs contained. In this time every byte counted on computers as storage was limited. Game designers thus chose to use procedural map generation in their games, making it more compact & increasing it's playability.
In modern times Procedural world generation (PWG) has become an increasingly popular trend, making the game significantly more playable, allowing new features such as dynamic difficulty as well as giving the user a unique and varied experience through every playthrough. Whilst these early Procedural World Generators (PWGs) were often crude & basic, often containing unnatural or machine-like terrain with little to no consistency and even fewer regards to good level design rules & guidelines, progress in this field has been slowly made to improve the performance and results of these algorithms.
Many new algorithms have come along to try to correct and improve on the pitfalls that these early algorithms contained. Most of these are slow in performance and require significant processing power to compute terrain in real-time. In addition to this many of the fast alternatives to these algorithms also suffer from failing to adequately create playable maps in regards to design rules as well as occasionally failing to create completable maps. Whilst many of these algorithms have come along to implement more humanistic map design criteria, many of these implementations have failed or provide marginal benefits to previously used PWG methods. As a result, development of such algorithms of PWG has been stagnant.
In this paper, we intend to explore such algorithms used in PWG and analyse what has been done well, evaluate each given method and through this propose and develop our own flexible programmatic procedural map generation function, intended to contain both variation, humanization as well as customizability, allowing developers to create better looking & overall more playable procedurally generated maps.
Current Solutions To Procedural World Generation (PWG) In Top-down Games
There have been numerous implementations of Procedural World Generation (PWG) functions in both the indie & professional game developer communities. Whilst most are adapted to their specific game engine & required application, the logic of such algorithms generally stays the same, being agnostic of languages and use cases. A generalized outline of some of the most popular PWG algorithms is listed below.
Markov Chains
Markov chains are one of the oldest yet most effective methods of Procedural world generation (PWG). This method has been widely used over the years and has had multiple different variations implemented in many multi-dimensional models.
Markov chains work through a statistical decision tree process. Through this, a state space is constructed with transitional properties between states such that the next state for each iteration is dependent on the current state. With terrain generation, the process expands outwards from a starting point and is evaluated by comparing the possible states of its neighbours.
Markov chains are one of the oldest yet most effective methods of Procedural world generation (PWG). This method has been widely used over the years and has had multiple different variations implemented in many multi-dimensional models.
Markov chains work through a statistical decision tree process. Through this, a state space is constructed with transitional properties between states such that the next state for each iteration is dependent on the current state. With terrain generation, the process expands outwards from a starting point and is evaluated by comparing the possible states of its neighbours.
As a result of this function, Markov chains due to their simplicity have been used in many popular 2D platform games, such as Angry Birds & Super Mario Run. People who have observed terrain generated by these chains have said that they cause aesthetically pleasing and consistent levels, however, this does not correlate with playability as Markov chains also suffer from the inability to distinguish map design rules and if a generated map is playable without a secondary backtracking or pathfinding algorithm.
Cellular Automata
Cellular Automata is a discrete mathematics-based model of computation based on finite states. The program functions by containing a grid with a list of cells each with its finite states, additionally, restrictions on such states can be programmatically added. The program once run, then executes iterations of the program based on the conditions of its adjacent neighbour cell based on the set of rules. Whilst this is primarily a model used in games for modeling environmental systems, like heat, rain & fluid flow. It has also been used in limited cases in PWG. Whilst this model isn't primarily intended or designed for PWG there has been a varying degree of success in using this model to create realistic albeit random-looking generated caves through this model.
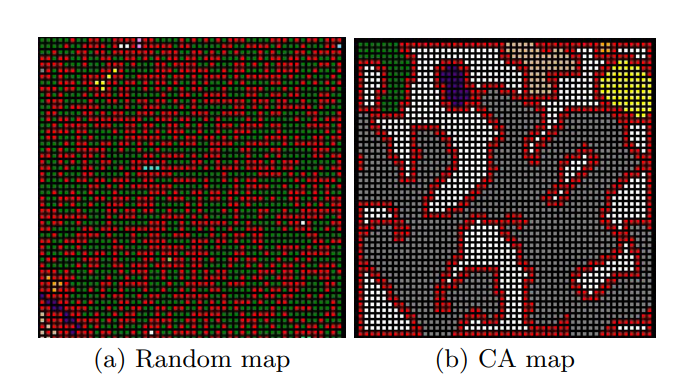
Figure 1: Johnson L, Cellular automata for real-time generation of infinite cave levels
Binary Space Partitioning (BSP)
Binary Space Partitioning (BSP) is a highly popular & utilized mapping technique used in multiple prominent games, like Counter-Strike: Global Offensive. BSP through a system of recursively dividing space, generates an object with the data structure of a BSP tree. Through these BSP mappers can create some of the simplest yet most prominent rouge-like dungeons - rectangular dungeon maps.
Through binary space partitioning, it allows the algorithm to split a space up into several randomly sized rectangles of where a pre-assembled room component will be placed. Through this dungeons can be formed. These separate dungeon rooms are then linked through a secondary backtracking algorithm that checks & ensures all associated dungeons rooms are linked together. From this, a highly detailed, randomized yet consistent & solvable dungeon can be generated.
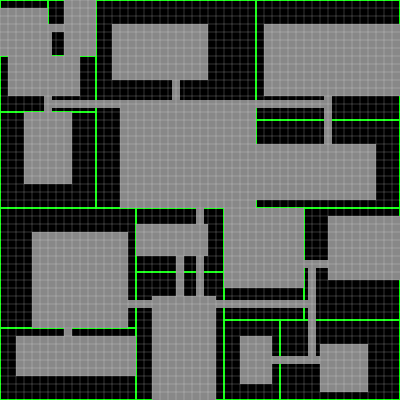
Figure 2: Dungeon Generation using BSP Trees
Machine Learning
Machine learning, unlike the algorithms mentioned previously, offers a unique approach to procedural world generation. Similar to Markov chains they are also heavily reliant on statistical modeling, however, differ as the procedurally generated output is based or transferred from the data-set it is trained on, giving it weighted biases. With Machine learning models such as Generative Adversarial Networks (GANs), the neural network is trained by being given a set of hand-generated maps which are then fed to the network capturing high-level features. From this, the model is further trained in 'learning' these high-level rules and interpolating them into a set of weights which allows it to generate its maps.
Whilst GANs also don't offer guaranteed playability in their maps and occasionally require back-tracking or pathfinding to fix/evaluate, these properties are often initiated by the data it is trained on, as such one of the rooms, it was trained on also contained this unsolvable feature. GANs additionally whilst following the high-level rules of map design and having great success in image generation, often fail to capture the nuisance structural features and details rooms created by mappers contain required for a well-defined level. This paired with the network requiring tens if not hundreds of pre-generated maps for training before the network can function as well as overall having lower success rates, being more complicated, less editable, being unpredictable & performance intensive compared to other functions have made machine learning models not a popular method of PWG in game development.
As a result, this approach isn't ideal for game developers generating new levels for their games, but rather for pre-existing games with community support. This allows the machine learning model to have a greater data set to base maps off and overall lowers the unpredictability of the model, with the increase of data proportionally increasing playability.
This approach, however, alternatively may be useful for other processes in procedural world generation such as in the difficulty evaluation & size evaluation sections. This as an additional tool to back-tracking & pathfinding may allow developers to more accurately determine & evaluate the difficulty of automatically generated maps without requiring to play them themselves. This in turn can minimize quality control issues as well as reduce the overall unplayability of maps from some of the other algorithms previously mentioned.
Comparative Benchmark Between Algorithms
| Technique | Pros | Cons |
|---|---|---|
| Markov Chains | Fast, aesthetically pleasing & varied, output statistically resembles similar things to its given components, reliant on clearly defined statistical properties (not a black box) | Reliant on statistical properties on a small scale, this fails to see long term dependency of the entire map and occasionally causes unsolvable maps, needs active repair function (such as backtracking) to fix unsolvable sections |
| Cellular Automata | Fast, simple, low cost, creates 'natural' looking cave environments | Unstructured, chaotic, lacks overarching control or long term understanding, cannot create dungeons, can create unsolvable levels & requires an active repair function |
| Machine Learning | High variety, capable of capturing statistical patterns of real levels, can recognize overarching level design patterns, requires minimal coding, can be reused for many applications with minimal editing | Requires an active repair function, is highly performance intensive in both CPU, Memory & RAM, often fails to capture underlying rules of a level, is a "black box" where the predicted output has no way of debugging or future understanding - i.e., an input comes in and an input goes out, requires huge data sets & clean training data to set up |
| BSP Trees | Good, highly effective, creates iconic cube dungeons, very easy to program, space aware, requires minimal fixing (back-tracking to add to pathways), is simplistic in concepts & very easy to debug & modify | Variation is limited, cannot create 'real' procedural maps (it is still pre-defined), levels are typically required to be rectangular / non-continuous |
Proposed Solution Using Wave Form Collapse (WFC) Functions
The proposed solution to the problem of creating realistic & detailed procedural worlds for top-down 2D games through programmatic procedural content generation is listed below.
Proposed Implementation Of WFC
Through the implementation of a relatively newly created algorithm, the Wave Form Collapse (WFC) function as well as adding elements of Machine Learning & Binary Space Partitioning we can create a robust, automatic algorithm capable of being highly flexible and modifiable to the developer.
Through utilizing the Wave Form Collapse function which works similar to Markov chains however also emulating entropy through its pseudo-quantum-mechanics inspired randomness it allows us to create seemingly random but humanized and aesthetically pleasing terrain maps.
This conjoined with Binary Space Partitioning, separating the square grid into sections where an individual WFC will run independently of one another, being later linked through backtracking and a machine model evaluating the finalized solution checking its difficulty & size, should create a highly unique but also highly structured procedural map for the users to traverse.
Benefits Of The Proposed Solution
Through this proposed algorithm we increase the overall success rates for the generated map to be playable without the need for backtracking or user intervention, in addition to us containing the distinct block structure Binary Space Partitioned maps have whilst including the humanistic, however, quasi-randomness the Wave Form Collapse provides.
As a result of this, our maps should contain distinctive & separated arenas for players to battle in whilst also having each room being uniquely generated & different, unlike most BSP based dungeons which use a sample set of pre-assembled dungeon rooms.
These maps are then evaluated, checked and given a ranking in both; difficulty, size, playability & aesthetics based on a machine learning neural network. Through this, we can ensure the generated map is of high quality and is proficient for a user to play, without being required to check the map beforehand. This ensures & allows the game developer to be positive that the resultant map is of quality for the user to play and assists in minimizing the pitfalls other algorithms such as Markov chains & Cellular Automata contain when developing maps.
Challenges Involved
The proposed algorithm above is quite a complex & quite intensive algorithm requiring heavy domain knowledge both on statistics & machine learning. Additionally to this, optimization and integration of these multiple systems may cause an issue and will require extensive Data Structures & Algorithms (DSA) knowledge.
A list of potential issues in this proposed algorithm is as listed below:
- Incompatibility / heavy dependencies on multiple programming languages. E.g. Python for machine learning, C# for WFC & BSP
- Issues with over-training / introducing biased or incorrect data into the machine learning model
- Balancing the reward functions & sensitivities for the weight functions
- Issues with creating a consistent map & debugging this due to it's randomized and procedural nature
- Allowing this code to be intuitive and flexible for other researchers & game developers to use
- Ensuring speed, accuracy & fidelity to the proposed algorithm as this requires multiple separate but highly connected systems
- Issues with logic/domain knowledge outside of the reach of the researcher, which may require consultancy from experts / the research supervisor
Conclusion
In this paper, we have explored the problem of creating realistic & varied programmatically procedurally generated maps using procedural world generation (PWG) in-depth for 2-dimensional top-down games. We have explored previously used solutions in the procedural world generation (PWG) field such as; BSP Trees, Cellular Automata & Machine learning. We have evaluated such methods and have proposed a new modified system emphasizing and collecting the advantages of all methods whilst trying to minimize the overall flaws these algorithms create such as occasionally creating unsolvable maps or undetailed and seemingly random unintuitive maps. From this paper, we are hopeful we can utilize the Wave Form Collapse (WFC) function to assist in making a more immersive & unique gaming experience in the future for users.
